Counting Polygons in Node Graphs

Motivation

  • This is what happens when you get curious about efficiently finding triangles in a node graph using linear algebra (instead of recursively walking the whole graph).

Features of custom GraphCounts class:

  1. Accepts node/edge data in dictionary format
  2. Plots the graph
  3. Counts the number of triangles, quadrilaterals, and pentagons.
  4. Optionally displays the polygons within the nodes of the graph.
  5. Written in python (view source code at bottom).

Author:

Examples

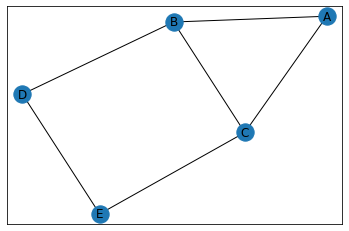
"House"

In [2]:
# Graph Data

# `data` maps a node to its set of neighbors
# note: if A has neighbor B, then not needed to specify that B has neighbor A
data = {
    'A':{'B', 'C'},
    'B':{'C', 'D'},
    'E':{'C', 'D'}
}

graph = GraphCounts(data, show_matrix=True, show_graph=True)

S1:
 [[0. 1. 1. 0. 0.]
 [1. 0. 1. 1. 0.]
 [1. 1. 0. 0. 1.]
 [0. 1. 0. 0. 1.]
 [0. 0. 1. 1. 0.]]
In [3]:
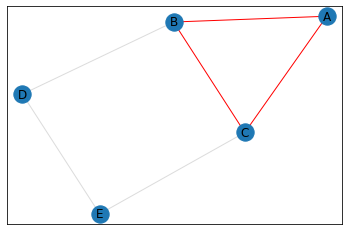
triangle_count = graph.count_triangles(show_plots=True)
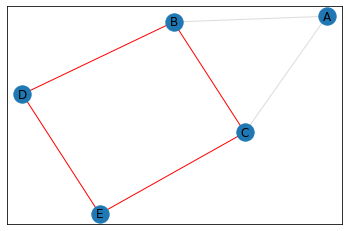
quad_count = graph.count_quads(show_plots=True)
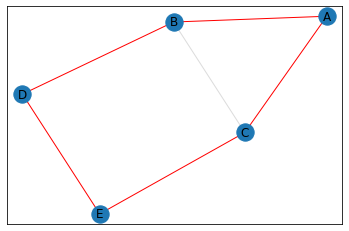
pentagon_count = graph.count_pentagons(show_plots=True)

print("\n\nCounts")
print("triangles count:", triangle_count)
print("quads count:", quad_count)
print("pentagons count:", pentagon_count)

Triangles

Quadrilaterals

Pentagons


Counts
triangles count: 1.0
quads count: 1.0
pentagons count: 1.0

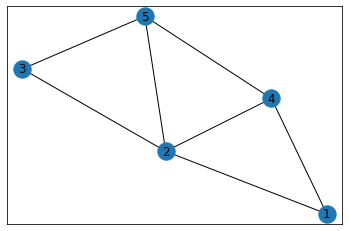
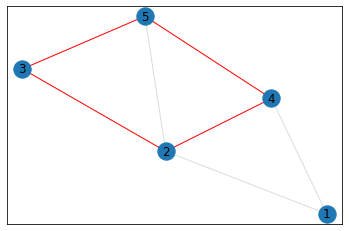
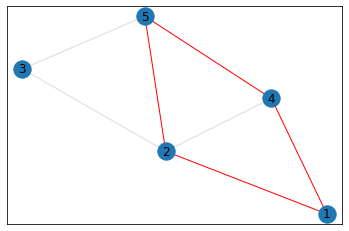
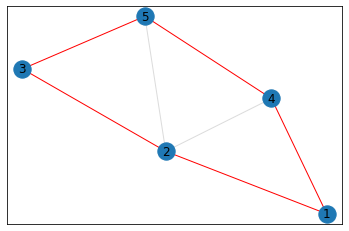
"Trapezoid"

In [4]:
data = {
    2:{1,3,4,5},
    3:{5},
    4:{1,5},
}

graph = GraphCounts(data)
In [5]:
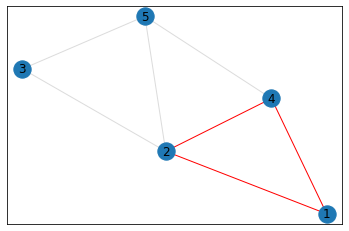
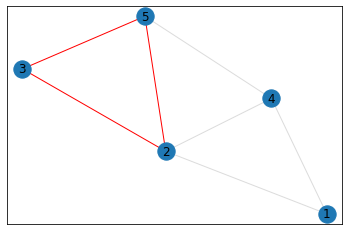
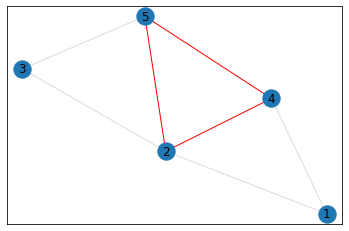
triangle_count = graph.count_triangles(show_plots=True)
quad_count = graph.count_quads(show_plots=True)
pentagon_count = graph.count_pentagons(show_plots=True)

print("\n\nCounts")
print("triangles count:", triangle_count)
print("quads count:", quad_count)
print("pentagons count:", pentagon_count)

Triangles

Quadrilaterals

Pentagons


Counts
triangles count: 3.0
quads count: 2.0
pentagons count: 1.0

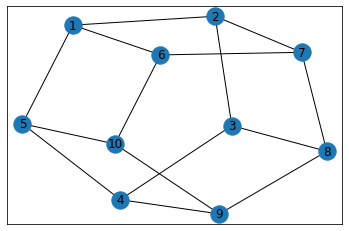
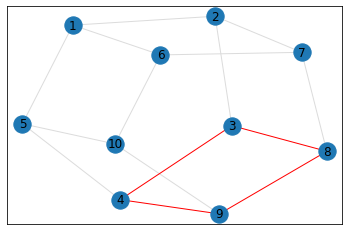
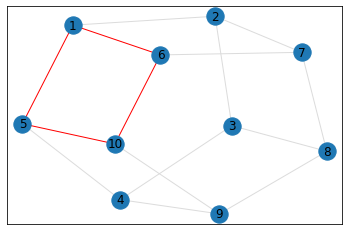
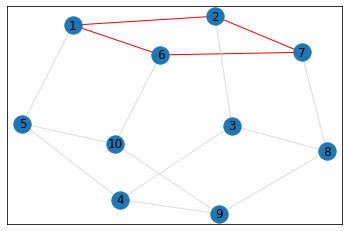
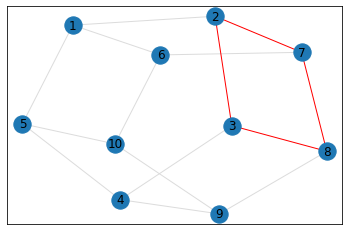
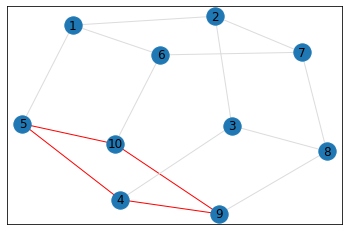
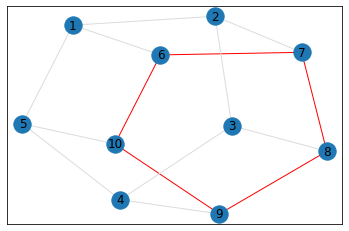
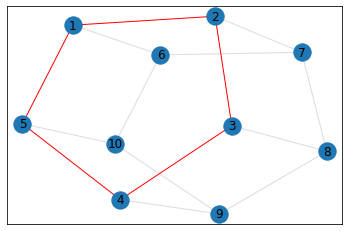
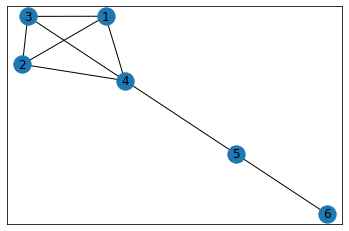
"Pentagonal Prism"

In [6]:
data = {
    1:{2,5,6},
    2:{3,7},
    3:{4,8},
    4:{5,9},
    5:{10},
    6:{7,10},
    8:{7,9},
    9:{10}
}

graph = GraphCounts(data)
In [7]:
triangle_count = graph.count_triangles(show_plots=True)
quad_count = graph.count_quads(show_plots=True)
pentagon_count = graph.count_pentagons(show_plots=True)

print("\n\nCounts")
print("triangles count:", triangle_count)
print("quads count:", quad_count)
print("pentagons count:", pentagon_count)

Triangles: none to show
Quadrilaterals

Pentagons


Counts
triangles count: 0.0
quads count: 5.0
pentagons count: 2.0

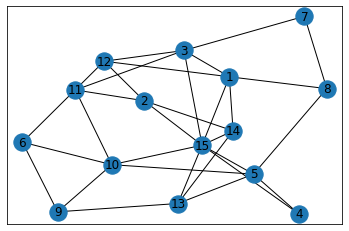
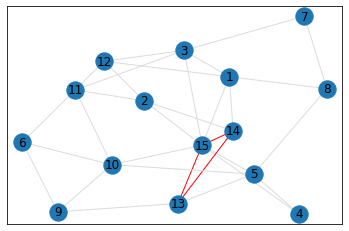
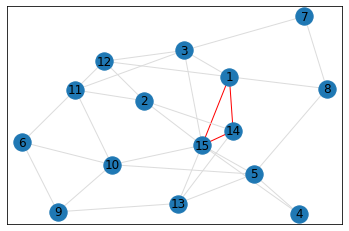
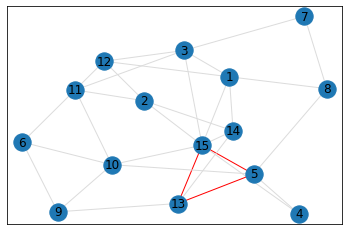
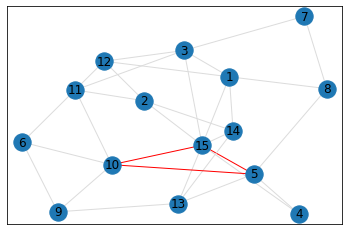
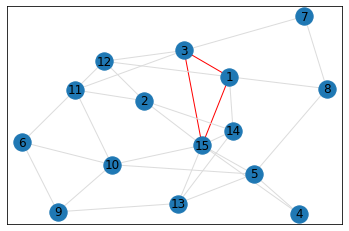
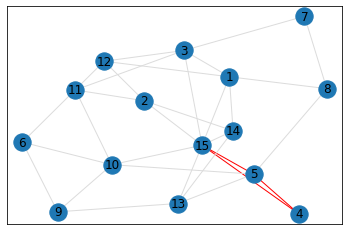
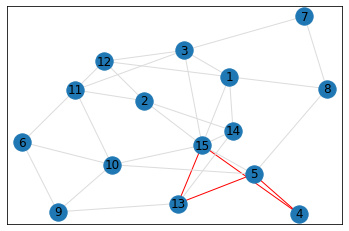
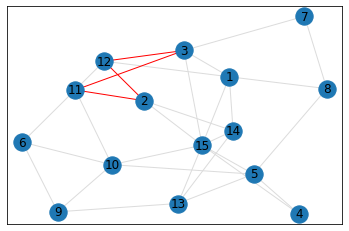
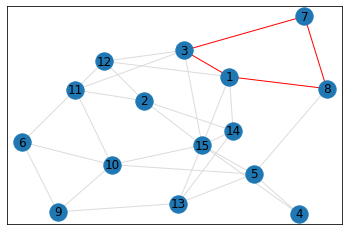
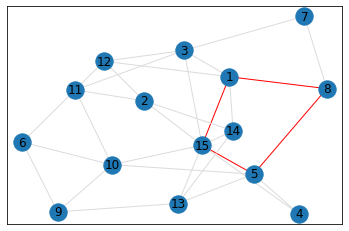
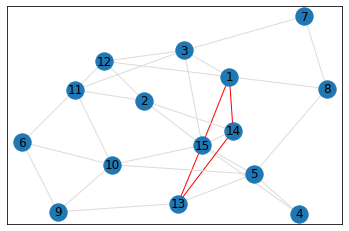
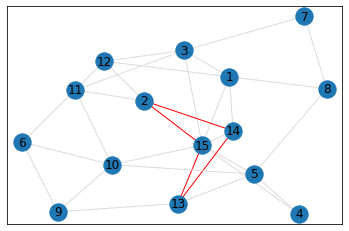
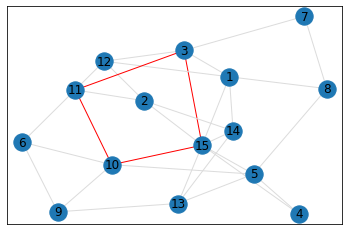
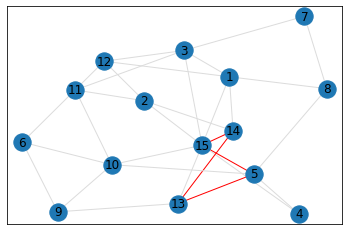
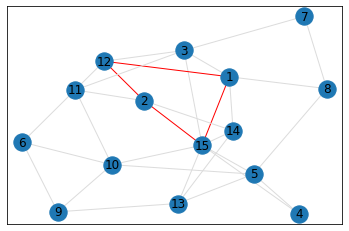
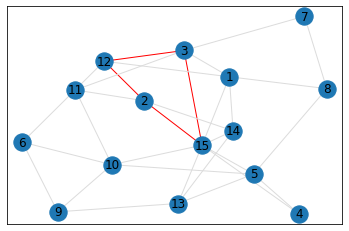
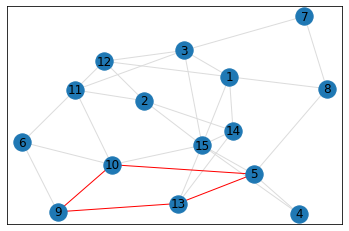
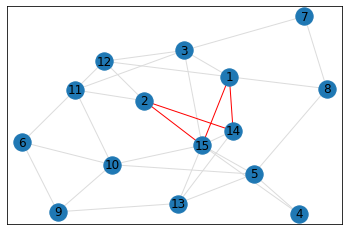
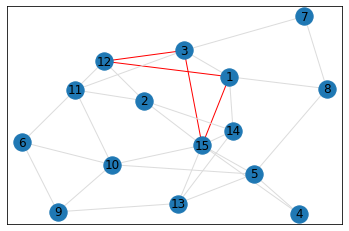
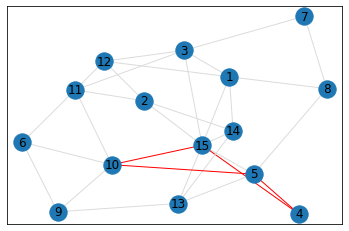
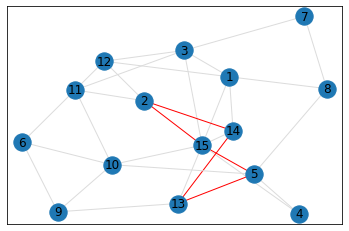
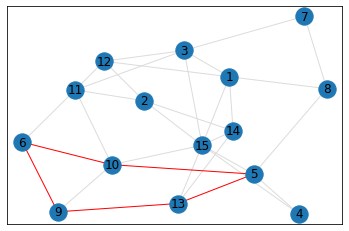
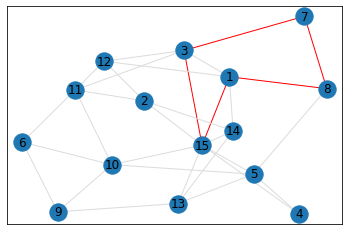
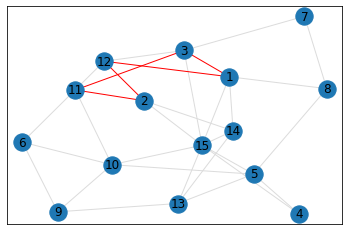
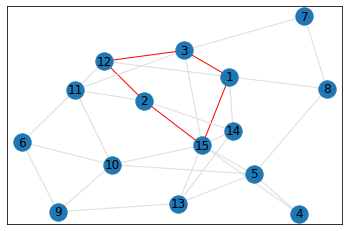
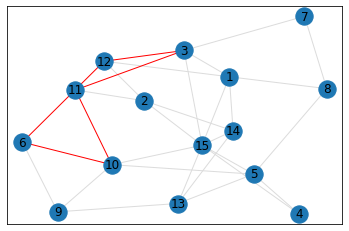
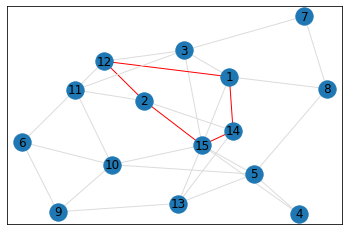
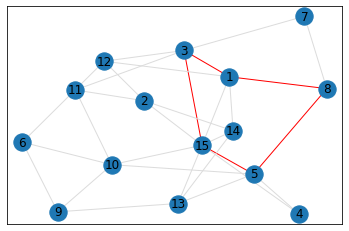
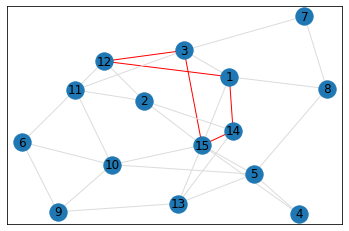
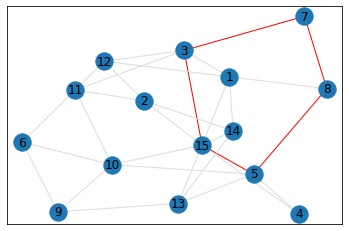
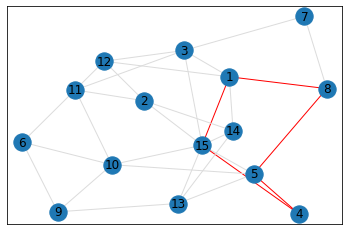
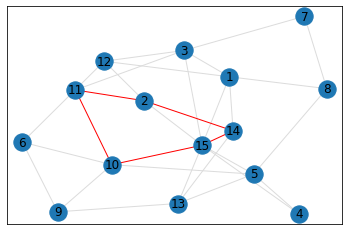
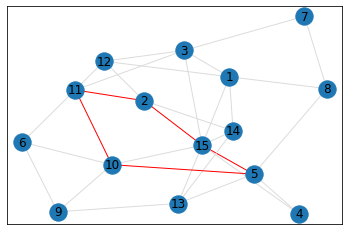
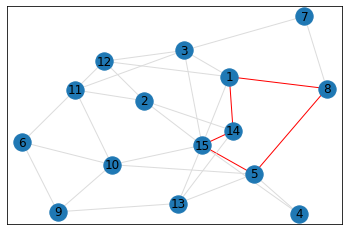
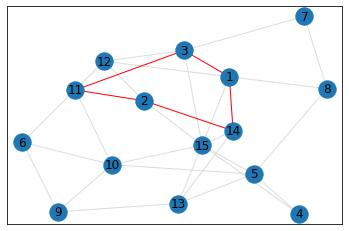
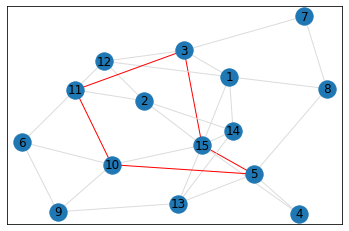
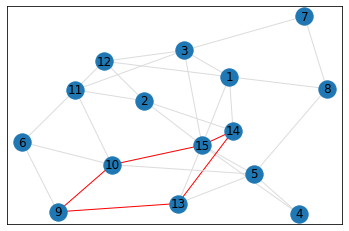
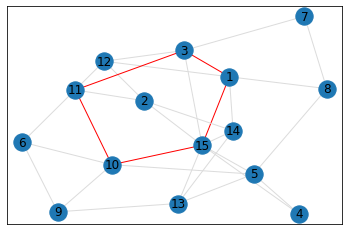
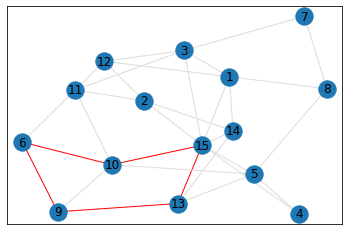
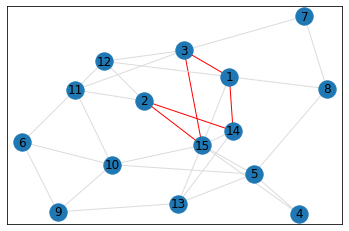
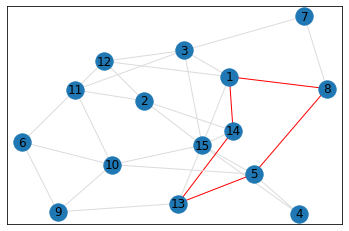
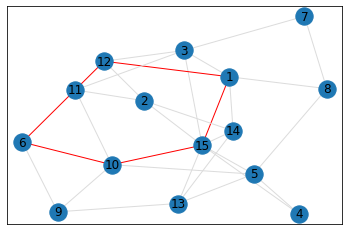
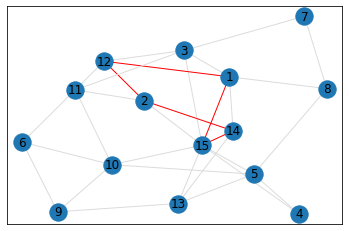
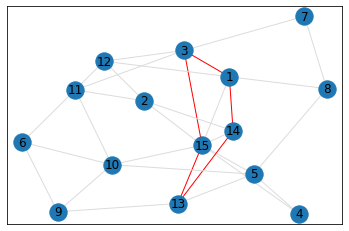
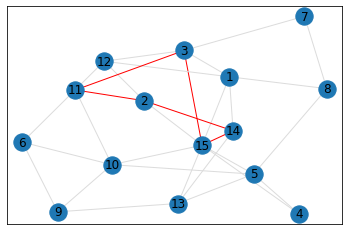
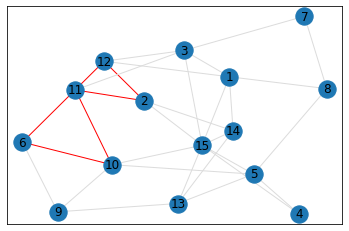
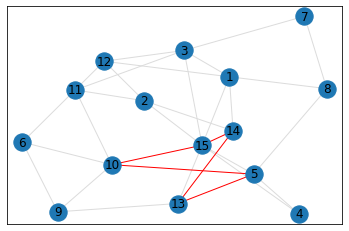
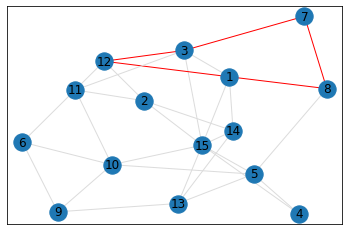
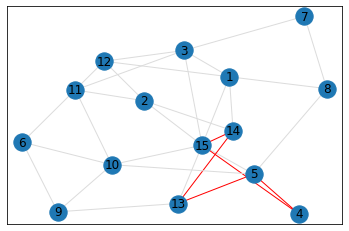
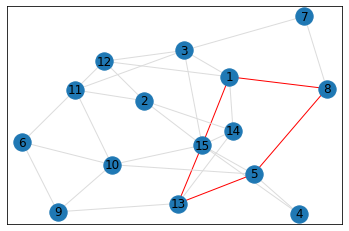
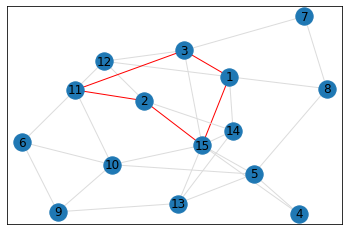
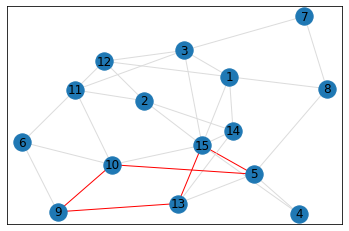
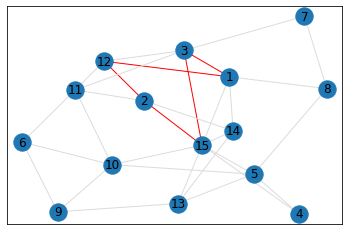
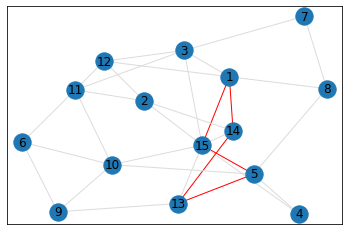
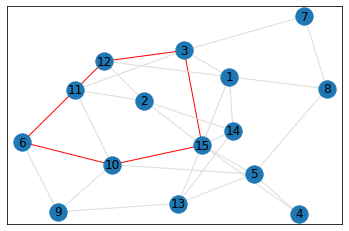
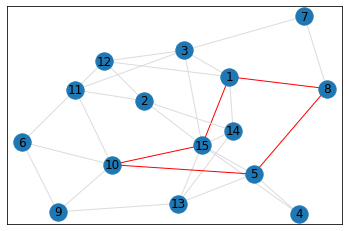
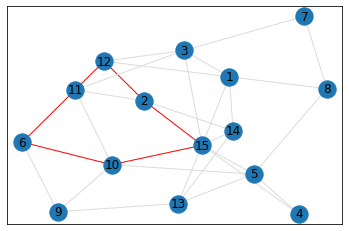
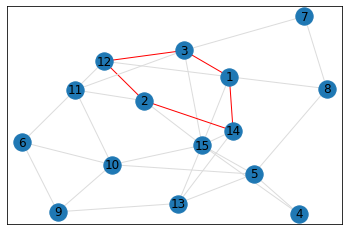
Random, 15 nodes

In [8]:
# generate random graph
data = make_random_graph_data(15, 3)
graph = GraphCounts(data)

Node count: 15, edge_count: 30, avg degree: 2.466666666666667
In [9]:
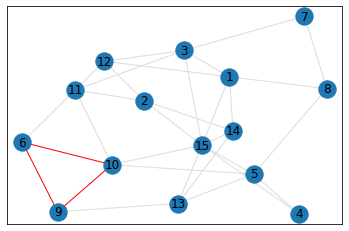
triangle_count = graph.count_triangles(show_plots=True)
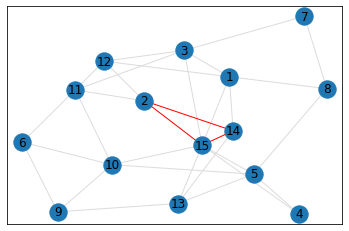
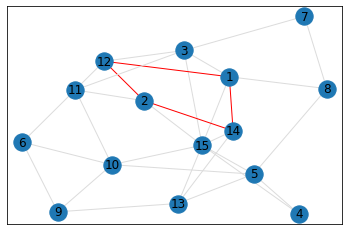
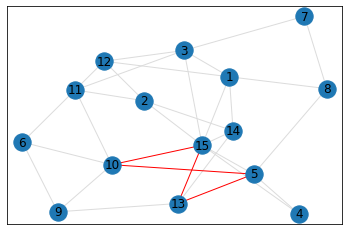
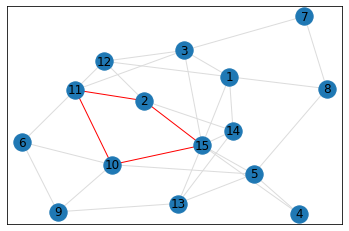
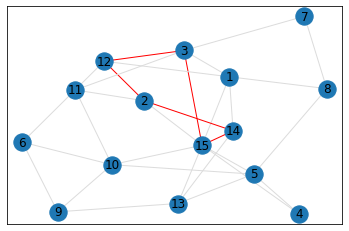
quad_count = graph.count_quads(show_plots=True)
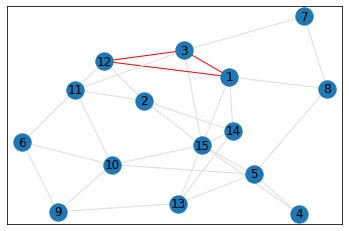
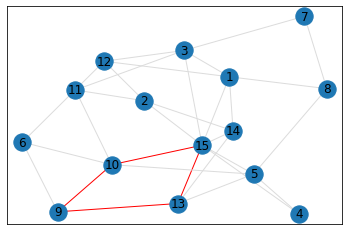
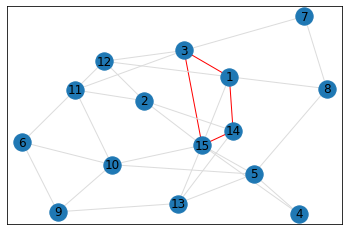
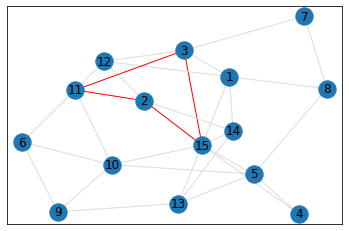
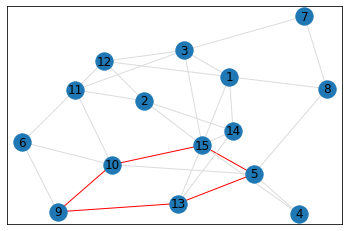
pentagon_count = graph.count_pentagons(show_plots=True)

print("\n\nCounts")
print("triangles count:", triangle_count)
print("quads count:", quad_count)
print("pentagons count:", pentagon_count)

Triangles

Quadrilaterals

Pentagons


Counts
triangles count: 9.0
quads count: 20.0
pentagons count: 40.0

Random, 1,000 nodes

A graph this large needs a much larger display, so graphs will not be shown in this example. But note the efficient execution times.

In [10]:
# generate random graph
data = make_random_graph_data(1000, 3)
graph = GraphCounts(data, show_matrix=False, show_graph=False)

# runtime: 356 milliseconds

Node count: 1000, edge_count: 1955, avg degree: 1.958
In [11]:
print("triangles:", graph.count_triangles())

print("quadrilaterals:", graph.count_quads())

print("pentagons:", graph.count_pentagons())

# runtime: 256 milliseconds

triangles: 6.0
quadrilaterals: 20.0
pentagons: 45.0

Random, 10,000 nodes

A graph this large needs a much larger display, so graphs will not be shown in this example. But note the efficient execution times.

In [20]:
# generate random graph
data = make_random_graph_data(10000, 3)
graph = GraphCounts(data, show_matrix=False, show_graph=False)

# runtime: 21.6 seconds

Node count: 10000, edge_count: 20030, avg degree: 2.0033
In [21]:
graph.count_triangles()

# runtime: 63.0 seconds
Out[21]:
9.0
In [22]:
graph.count_quads()

# runtime: 57.2 seconds
Out[22]:
21.0
In [23]:
graph.count_pentagons()

# runtime: 89.1 seconds
Out[23]:
79.0

Other Examples

"Kite"

In [25]:
data = {
    1:{2,3,4},
    2:{1,3,4},
    3:{1,2,4},
    4:{1,2,3},
    5:{4,6}
}

graph = GraphCounts(data)
In [28]:
print("triangles:", graph.count_triangles())
print("quadrilaterals:", graph.count_quads())
print("pentagons:", graph.count_pentagons())

triangles: 4.0
quadrilaterals: 3.0
pentagons: 0.0

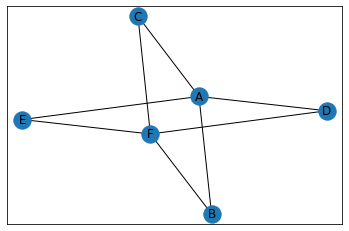
"Ninja Star"

In [30]:
data = {
    'A': {'B', 'C', 'D', 'E'},
    'F': {'B', 'C', 'E', 'D'},
}

graph = GraphCounts(data)
In [31]:
print("triangles:", graph.count_triangles())
print("quadrilaterals:", graph.count_quads())
print("pentagons:", graph.count_pentagons())

triangles: 0.0
quadrilaterals: 6.0
pentagons: 0.0

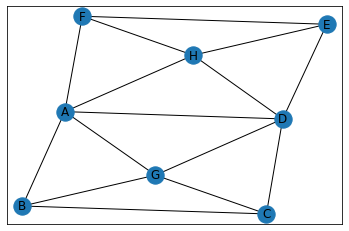
"Two Windows"

In [32]:
data = {
    'A':{'B', 'G', 'D', 'H', 'F'},
    'B':{'C', 'G'},
    'C':{'G'},
    'D':{'C', 'G', 'H', 'E'},
    'E':{'H'},
    'F':{'H', 'E'},
}

graph = GraphCounts(data)
In [33]:
print("triangles:", graph.count_triangles())
print("quadrilaterals:", graph.count_quads())
print("pentagons:", graph.count_pentagons())

triangles: 8.0
quadrilaterals: 11.0
pentagons: 14.0

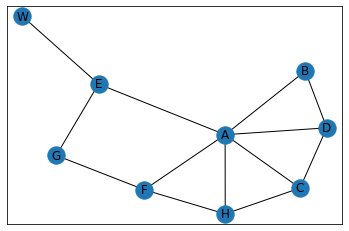
"Baby Carriage"

In [34]:
# maps a node to its set of neighbors
# note: if A has neighbor B, then not needed to specify that B has neighbor A

# rects with triangles
data = {
    'A': {'B','C', 'D', 'E', 'F'},
    'D': {'B', 'C'},
    'G': {'E', 'F'},
    'H': {'A', 'C', 'F'},
    'E': {'W'}
}

graph = GraphCounts(data)
In [35]:
print("triangles:", graph.count_triangles())
print("quadrilaterals:", graph.count_quads())
print("pentagons:", graph.count_pentagons())

triangles: 4.0
quadrilaterals: 4.0
pentagons: 3.0

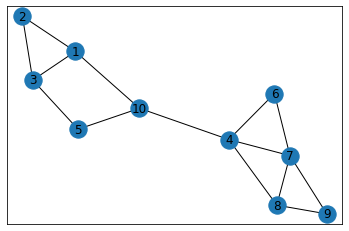
"Bipolar"

In [36]:
data = {
    1:{2,3,10},
    3:{2,5},
    5:{10},
    10:{4},
    4:{6,7,8},
    7:{6,8,9},
    8:{9}
}

graph = GraphCounts(data)
In [37]:
print("triangles:", graph.count_triangles())
print("quadrilaterals:", graph.count_quads())
print("pentagons:", graph.count_pentagons())

triangles: 4.0
quadrilaterals: 3.0
pentagons: 2.0

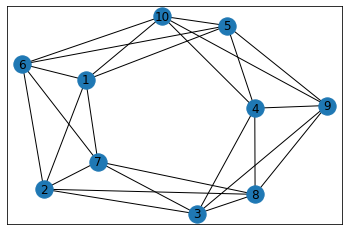
"Sand Dollar"

In [39]:
# star
data = {
    1:{2,5,6,7,10},
    2:{3,6,7,8},
    3:{4,7,8,9},
    4:{5,8,9,10},
    5:{6,9,10},
    6:{7,10},
    8:{7,9},
    9:{10}
}

graph = GraphCounts(data)
In [40]:
print("triangles:", graph.count_triangles())
print("quadrilaterals:", graph.count_quads())
print("pentagons:", graph.count_pentagons())

triangles: 20.0
quadrilaterals: 35.0
pentagons: 72.0

Source Code

Written by Doug Issichopoulos, dougissi.com

Feb 10, 2020

In [1]:
import pandas as pd
import numpy as np
import networkx as nx
from collections import defaultdict
import random
import matplotlib.pyplot as plt


def symmetrify_dict_of_dicts(dict_of_dicts):
    sym_dict = defaultdict(dict, dict_of_dicts)
    for k, v in dict_of_dicts.items():
        for x, y in v.items():
            sym_dict[x][k] = y
    return dict(sym_dict)


def symmetrify_dict_of_sets(dict_of_sets):
    sym_dict = defaultdict(set, dict_of_sets)
    for k, v in dict_of_sets.items():
        for x in v:
            sym_dict[x].add(k)
    return dict(sym_dict)


def matrix_multiplication(x, y):
    return np.matmul(x, y)


def matrix_to_power(S, n):
    Sn = S  # initialize output
    while n > 1:
        Sn = matrix_multiplication(Sn, S)
        n -= 1
    return Sn


def get_matrix_diagonal_dict(S, nodes):
    '''`nodes` should be ordered the same as the rows/columns of `S`'''
    return {node: val for node, val in zip(nodes, S.diagonal())}


def make_random_graph_data(node_count, max_initial_neighbors):
    all_nodes = list(range(1, node_count+1))

    data = {}
    for node in all_nodes:
        all_other_nodes = set(all_nodes).difference({node})
        rand_num_neighbors = random.randrange(1,max_initial_neighbors+1)

        data[node] = set(random.sample(all_other_nodes, rand_num_neighbors))

    # print counts of nodes and edges, as well as avg degree, to console
    all_edges = set()
    degs = []
    for node1, edges_set in data.items():
        for node2 in edges_set:
            all_edges.add(tuple(sorted([node1, node2])))
        degs.append(len(edges_set))
    print(f'Node count: {len(all_nodes)}, edge_count: {len(all_edges)}, avg degree: {sum(degs)/len(degs)}')

    return data


class GraphCounts(object):
    def __init__(self, data, show_matrix=False, show_graph=True):
        '''
        data can be dict from node -> {neighbor set}, or node -> {neighbor1: weight, neighbor2: weight,...}, 
        where if B is a neighbor of A, no need to define A as neighbor of B, as weights are ignored.
        '''
        self.data_dict = symmetrify_dict_of_dicts({k:{x:1 for x in list(v) if x != k} for k, v in data.items()})

        # make pandas DataFrame of graph data
        df = pd.DataFrame(self.data_dict).fillna(0)
        df.sort_index(inplace=True)
        df.sort_index(axis=1, inplace=True)
        self.df = df

        # make matrix
        self.S1 = df.values
        if show_matrix:
            print('S1:\n',self.S1)

        # optionally plot graph data using networkx
        if show_graph:
            self.G, self.pos = self._define_graph()
            nx.draw_networkx(self.G, pos=self.pos)
            plt.show()

    def _define_graph(self):
        G = nx.Graph(self.df)
        pos = nx.spring_layout(G)
        return G, pos

    def _get_triangles_dict(self, S3):
        returning_3_walks_dict = get_matrix_diagonal_dict(S3, self.df.index)
        return {k: v / 2 for k, v in returning_3_walks_dict.items()}

    @staticmethod
    def _get_nodes_set_with_unidentified_polygons(polygons_dict):
        return {node for node, polygon_count in polygons_dict.items() if polygon_count > 0}

    @staticmethod
    def _polygon_data_to_tuple(data):
        '''
        data should be dict from node -> {neighbor set}, 
        where if B is a neighbor of A, no need to define A as neighbor of B
        '''

        sym_dict = symmetrify_dict_of_sets(data)

        nodes = set()
        edges = set()
        for node, edges_set in sym_dict.items():
            nodes.add(node)
            for edge in edges_set:
                edges.add(tuple(sorted({node, edge})))

        return (tuple(sorted(nodes)), tuple(sorted(edges)))

    def _identify_polygons(self, polygon_type, polygons_dict):

        # helper function
        def build_polygons_set(simplified_data_dict, polygon_type, polygons_set, polygons_dict):
            '''
            Builds `polygons_set` via recursion, based on number of polygons calculated at each node (from `polygons_dict`)
            '''

            for node1, node1_neighbors in simplified_data_dict.items():
                for node2 in list(node1_neighbors):
                    node2_neighbors = simplified_data_dict[node2]

                    other_node1_neighbors = node1_neighbors.difference({node2})
                    other_node2_neighbors = node2_neighbors.difference({node1})

                    if polygon_type == 'triangle':
                        triangles = set()
                        common_neighbors = other_node1_neighbors.intersection(other_node2_neighbors)
                        for node3 in list(common_neighbors):
                            triangle = self._polygon_data_to_tuple({
                                node1: {node2, node3},
                                node2: {node3}
                            })
                            if triangle not in polygons_set:
                                triangles.add(triangle)
                        polygons = triangles

                    elif polygon_type == 'quad':
                        connections = set()
                        quads = set()
                        for node3 in list(other_node1_neighbors):
                            for node4 in list(other_node2_neighbors):
                                if node3 != node4 and node4 in simplified_data_dict[node3]: # nodes different and connection exists between them
                                    connection = tuple(sorted([node3, node4]))
                                    if connection not in connections:  # if new connection then valid polygon
                                        connections.add(connection)
                                        quad = self._polygon_data_to_tuple({
                                            node1: {node2, node3},
                                            node2: {node4},
                                            node3: {node4}
                                        })
                                        if quad not in polygons_set:
                                            quads.add(quad)
                        polygons = quads

                    elif polygon_type == 'pentagon':
                        connections = set()
                        pentagons = set()
                        for node3 in list(other_node1_neighbors):
                            for node4 in list(other_node2_neighbors):
                                if node3 != node4: # nodes different
                                    common_neighbors = set(simplified_data_dict[node3]).intersection(simplified_data_dict[node4]).difference({node1,node2,node3,node4})
                                    for node5 in common_neighbors:
                                        connection = tuple(sorted([node3, node4, node5]))
                                        if connection not in connections:  # if new connection then valid polygon
                                            connections.add(connection)
                                            pentagon = self._polygon_data_to_tuple({
                                                node1: {node2, node3},
                                                node2: {node4},
                                                node3: {node5},
                                                node4: {node5}
                                            })
                                            if pentagon not in polygons_set:
                                                pentagons.add(pentagon)
                        polygons = pentagons

                    else:
                        raise ValueError(f"Polygon type '{polygon_type}' not valid.")

                    if not polygons:
                        continue

                    # update storages based on new polygons
                    for polygon in polygons:

                        # add polygon to storage
                        polygons_set.add(polygon)

                        # decrement count of unidentified polygons at node, for each node in polygon
                        nodes, _ = polygon
                        for node in nodes:
                            polygons_dict[node] -= 1

                    return


        ## main function

        # raise error if invalid polygon type
        valid_polygon_types = {'triangle', 'quad', 'pentagon'}
        if polygon_type not in valid_polygon_types:
            raise ValueError(f"Polygon type '{polygon_type}' not valid -- must be among: {valid_polygon_types}")

        polygons_dict = dict(polygons_dict)  # make copy to avoid mutilation

        nodes_set_with_unidentified_polygons = self._get_nodes_set_with_unidentified_polygons(polygons_dict)

        simplified_data_dict = {k:{x for x, _ in v.items() if x in nodes_set_with_unidentified_polygons}
                                for k, v in self.data_dict.items()
                                if k in nodes_set_with_unidentified_polygons}

        polygons_set = set()
        while True:
            build_polygons_set(simplified_data_dict, polygon_type, polygons_set, polygons_dict)

            # limit search based on found polygons above
            nodes_set_with_unidentified_polygons = self._get_nodes_set_with_unidentified_polygons(polygons_dict)
            if not nodes_set_with_unidentified_polygons:
                break

            simplified_data_dict = {k:{x for x in v if x in nodes_set_with_unidentified_polygons}
                                    for k, v in simplified_data_dict.items()
                                    if k in nodes_set_with_unidentified_polygons}

        return polygons_set

    def _plot_polygons(self, polygons_set, desc):

        def show_original_graph(G, pos):
            print('Original')
            nx.draw_networkx(G, pos=pos)
            plt.show()

        # if graph wasn't originally drawn, define it
        if not hasattr(self, 'G') or not hasattr(self, 'pos'):
            self.G, self.pos = self._define_graph()
            if not polygons_set:  # if no polygons to plot, show original anyway
                show_original_graph(self.G, self.pos)

        # if no polygons to plot, inform user and return
        if not polygons_set:
            print(f'{desc}: none to show')
            return

        all_graph_edges = [tuple(sorted(edge)) for edge in self.G.edges]

        # plot each polygon
        print(desc)
        for _, edges in polygons_set:
            polygon_edges = set(edges)
            edge_colors = ["red" if edge in polygon_edges else "gainsboro" for edge in all_graph_edges]
            nx.draw_networkx(self.G, pos=self.pos, edge_color=edge_colors)
            plt.show()

    def count_triangles(self, show_plots=False):
        S3 = matrix_to_power(self.S1, 3)

        if show_plots:
            triangles_dict = self._get_triangles_dict(S3)
            triangles_set = self._identify_polygons('triangle', triangles_dict)
            self._plot_polygons(triangles_set, 'Triangles')

        return np.trace(S3) / 6

    def count_quads(self, show_plots=False):
        S2 = matrix_to_power(self.S1, 2)
        S4 = matrix_to_power(S2, 2)

        degrees_dict = get_matrix_diagonal_dict(S2, self.df.index)
        returning_4_walks_dict = get_matrix_diagonal_dict(S4, self.df.index)

        # make dict mapping a node to the count of all quadrilaterals passing it
        quads_dict = {}
        for node in self.data_dict.keys():
            quads_dict[node] = 0  # assume none unless proven otherwise

            returning_4_walks_at_node = returning_4_walks_dict[node]
            if returning_4_walks_at_node < 8:
                continue

            deg = degrees_dict[node]
            if deg < 2:
                continue

            sum_neighbor_degs = sum([degrees_dict[neighbor] for neighbor in self.data_dict[node]])
            if sum_neighbor_degs < 4:
                continue

            quads_dict[node] = (returning_4_walks_at_node - (deg * (deg - 1) + sum_neighbor_degs)) / 2

        if show_plots:
            quads_set = self._identify_polygons('quad', quads_dict)
            self._plot_polygons(quads_set, 'Quadrilaterals')

        return sum(quads_dict.values()) / 4  # account for double counting for each of quad's 4 nodes

    def count_pentagons(self, show_plots=False):
        S2 = matrix_to_power(self.S1, 2)
        S3 = matrix_multiplication(S2, self.S1)
        S5 = matrix_multiplication(S3, S2)

        returning_5_walks_dict = get_matrix_diagonal_dict(S5, self.df.index)

        # get list of triangles
        triangles_dict = self._get_triangles_dict(S3)
        triangles = self._identify_polygons('triangle', triangles_dict)

        # make map from node to list of triangles at that node
        triangles_at_nodes_dict = {node: [] for node in self.data_dict}
        for triangle in triangles:
            nodes, _ = triangle
            for node in nodes:
                triangles_at_nodes_dict[node].append(nodes)

        pentagons_dict = {}
        for node in self.data_dict.keys():
            pentagons_dict[node] = 0  # assume none unless proven otherwise

            returning_5_walks_dict_at_node = returning_5_walks_dict[node]
            if returning_5_walks_dict_at_node < 2:
                continue

            triangles_at_node = triangles_at_nodes_dict[node]

            # walks from triangles at node
            walks_from_triangles_at_node = 10 * len(triangles_at_node)

            # walks from all edges adjacent to triangles at node
            walks_from_edges_adj_to_triangles_at_node = 0  # initialize
            for triangle in triangles_at_node:

                # walks from edges from node not part of triangle
                tri_neighbors = set(triangle).difference({node})
                other_node_neighbors = set(self.data_dict[node]).difference(tri_neighbors)
                walks_from_edges_at_node_adj_to_triangle_at_node = 4 * len(other_node_neighbors)

                # walks from edges leaving triangle (not at node)
                tri_1, tri_2 = tri_neighbors
                other_neighbors_tri_1 = set(self.data_dict[tri_1]).difference({node, tri_2})
                other_neighbors_tri_2 = set(self.data_dict[tri_2]).difference({node, tri_1})
                walks_from_edges_NOT_at_node_adj_to_triangle_at_node = 2 * (len(other_neighbors_tri_1)
                                                                            + len(other_neighbors_tri_2))

                walks_from_edges_adj_to_triangles_at_node += (walks_from_edges_at_node_adj_to_triangle_at_node
                                                              + walks_from_edges_NOT_at_node_adj_to_triangle_at_node)


            # walks from single edges connecting node to other triangles
            walks_from_single_edges_connecting_node_to_other_triangles = 0
            for neighbor in self.data_dict[node]:
                disjoint_neighbor_triangles = [tri for tri in triangles_at_nodes_dict[neighbor] if node not in tri]
                walks_from_single_edges_connecting_node_to_other_triangles += (2 * len(disjoint_neighbor_triangles))

            # formula
            pentagons_dict[node] = (returning_5_walks_dict_at_node
                                    - (walks_from_triangles_at_node
                                       + walks_from_edges_adj_to_triangles_at_node
                                       + walks_from_single_edges_connecting_node_to_other_triangles)
                                   ) / 2

        if show_plots:
            pentagons_set = self._identify_polygons('pentagon', pentagons_dict)
            self._plot_polygons(pentagons_set, 'Pentagons')

        return sum(pentagons_dict.values()) / 5  # account for double counting for each of pentagon's 5 nodes